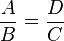"THALES DE MILETO"
Biografía.-
 |
| Thales de Mileto |
Filósofo y científico griego, nació y murió en Tales, polis griega en la costa de Jonia (hoy en día en Turquía). Nacimiento alrededor del 625/4 a. C. y muerte alrededor del 547/546 a. C. En su juventud viajó a Egipto, donde aprendió geometría de los
sacerdotes de Menfis, y astronomía, que posteriormente enseñaría con el
nombre de astrosofía. Fue el iniciador de la escuela filosófica milesia a la que pertenecieron, también, varios discipulados suyos. En la antigüedad se le consideraba uno de los Siete Sabios de Grecia, no se conserva ningún fragmento suyo y es probable que no dejara ninguno escrito en su muerte. Se le atribuyen desde el siglo V antes de cristo importantes aportaciones en el terreno de la filosofía, las matemáticas, astronomía, física, etc.. Así como un activo papel como legislador en su ciudad natal. Fue el primer filósofo griego que intentó dar una explicación física del
Universo, que para él era un espacio racional pese a su aparente
desorden. Sin embargo, no buscó un Creador en dicha racionabilidad, pues
para él todo nacía del agua, la cual era el elemento básico del que
estaban hechas todas las cosas, pues se constituye en vapor, que es
aire, nubes y éter; del agua se forman los cuerpos sólidos al
condensarse, y la Tierra flota en ella.
Tales es considerado el iniciador de la especulación científica y filosófica griega y occidental, aunque su figura y aportaciones están rodeadas de grandes incertidumbres.
Se conoce que Tales comenzó a utilizar el pensamiento deductivo aplicado a la geometría y se le atribuyen los nombres de dos teoremas geométricos que llevan su nombre.
Logros matemáticos.-
Existen dos teoremas de la geometría clásica que reciben su nombre, como ya hemos dicho antes, "Teorema de Thales" ambos atribuidos al matemático griego en el siglo XV a. C. Estos son:
Primer teorema. Explica esencial mente la forma de construir un triángulo semejante a uno ya existente (los triángulos semejantes son los que tienen iguales ángulos y sus lados homólogos proporcionales). El primer teorema de Tales recoge uno de los resultados más básicos de la geometría, este es:
Si en un triángulo se traza una línea paralela a cualquiera de sus
lados, se obtiene un triángulo que es semejante al triángulo dado.
Por el teorema de Tales ambos triángulos son semejantes, se cumple que:
Segundo teorema. Este es un teorema de geometría particularmente enfocado a los triángulos rectángulos, las circunferencias y los ángulos inscritos, consiste en "Sea B un punto de la circunferencia de diámetro AC, distinto de A y de C. Entonces el triángulo ABC, es un triángulo rectángulo".
En la circunferencia O y radio r, los segmentos OA, OB Y OC son iguales por ser todos radios de la misma circunferencia.Por lo tanto los triángulos AOB y BOC son isosceles.
·La suma de los ángulos del triángulo ABC es:
·Dividiendo ambos miembros de la ecuación anterior por dos, obtenemos:
Con la expresión anterior el teorema queda demostrado.
Aplicaciones en la ESO.-
Este teorema se utiliza mucho en la ESO y más aún en bachiller, porque es una forma mas sencilla y fácil de hallar los resultados. Se comienza a dar en cuarto, y sin algunos de estos dos teoremas es complicado que se haga algo, ya que son básicos.
-